

Geometry Study based on the Square-root-of-2 Ratio, Golden Ratio, and Ratios of Their Respective Groups
Research Field [1]
The author has been doing geometry study with focus on the golden ratio, square-root-of-2 ratio, golden square ratio, and square-root-of-2 square ratio, etc. which represent special mathematical ratios. These are all irrational numbers except the square-root-of-2 square ratio. Their respective values with four places of decimals are as follows:
Golden ratio —————— 1 : 1.6180
Square-root-of-2 ratio —— 1 : 1.4142
Golden square ratio ——— 1:2.6180
Square-root-of-2 square ratio ———– 1:2.0000
The golden square ratio is equal to the square of the golden ratio and its decimal figures are totally the same as those of the golden ratio. The square-root-of-2 square ratio is equal to the square of the silver ratio. The golden rhombus, square-root-of-2 rhombus, golden square rhombus, and square-root-of-2 square rhombus represent the rhombus whose diagonals are respectively in the golden ratio, square-root-of-2 ratio, golden square ratio, and square-root-of-2 square ratio. Also, the square-root-of-2 square rectangle and the golden rectangle are those whose side lengths are in the square-root-of-2 square ratio and golden ratio, respectively.
While the golden ratio has been well known since the ancient Greece age and has already been studied in depth by many researchers, the square-root-of-2 ratio and other ratios of this group have gone largely unnoticed until now, despite the fact that the rhombic dodecahedron, one of the most important polyhedra, is based on the square-root-of-2 ratio. According to a popular theory, these ratios are independent of one another. Against it, however, the author found out that there exists close relationship between the ratios of the golden ratio group and those of the square-root-of-2 ratio group through careful study on three kinds of rhombic polyhedron.
In advancing these researches, various advices have been given from such distinguished mathematicians as Ikuro Sato, Shin Hitotsumatsu, Koji Miyazaki, Jin Akiyama, and late Yasunari Watanabe. They have proved to be highly instrumental for me in proceeding with my study. Especially, Mr. Sato has kindly provided me with a lot of time-consuming support including calculations of dihedral of newly-created polyhedra. I am greatly thankful to them.
Great Pyramid
The Great Pyramid of Giza, Egypt is based on both the golden ratio and the square-root-of-2 ratio. It is generally believed to be in the shape of regular quadrangular pyramid. This is not true. In actuality, the Great Pyramid is in the shape of octahedron. It is equal to two units of regular quadrangular pyramid joined together with their square base in common. It can also be said that the Great Pyramid consists of four golden rhombuses which are mountain folded along the shorter diagonals. These rhombuses share the same two vertices of acute angle. The silver ratio is included in the square base.
Study Outcome
The fruits of the above-mentioned study are summarized below.
- Until now, it has been the established theory that the golden ratio is an independent ratio with no specific relationship with other special ratios like the square-root-of-2 ratio. It has been found, however, that dihedrals of solids transformed from three kinds of rhombic polyhedron are in perfect agreement and that there exist two sets of such dihedrals. They are the rhombic dodecahedron, rhombic triacontahedron, and rhombic enneacontahedron. The processes used for such transformation are: (1) golden transformation and (2) square-root-of-2 transformation, which are both very simple.
- The rhombic triacontahedron, and the rhombic enneacontahedron are totally different from each other in shape, face composition, etc. Nevertheless, the square-root-of-2 transformation of these solids has amazingly resulted in exactly the same shape.
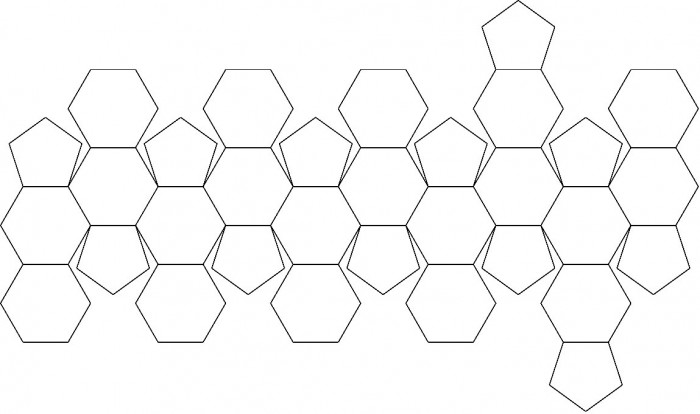
- Plane-filling is realized by the combination of the golden rhombus and the square-root-of-2 square rhombus. Another plane-filling becomes possible with the combination of the square-root-of-2 rhombus and the dodecagon ratio rhombus.
- The foregoing discussion clearly indicates that there exists a close relationship between the ratios of the golden ratio group and those of the square-root-of-2 ratio group, specifically between the golden ratio and the square-root-of-2 ratio and between the golden square ratio and the square-root-of-2 triplicate ratio, and between the golden ratio and the square-root-of-2 square ratio.
- There are several specific ratios of significance other than the golden ratio and the square-root-of-2 ratio, which however belong to either a golden ratio group or a square-root-of-2 ratio group.
- Except the square-root-of-2 triplicate ratio, these ratios are all equal to the length ratio of one side of the regular polygon to a specific diagonal thereof. Only the square-root-of-2 triplicate ratio is equal to the length ratio of one-half side of the regular octahedron to its space diagonal.
- They also represent the length ratios between two diagonals of specific rhombuses, and such rhombuses constitute specific rhombic polyhedron.
These discoveries are described in a mathematical paper. It was accepted by FORMA, an English scientific journal published by Society for Science on Form, Japan and published on the web in mid-March, 2021. Please refer to Forma, Vol. 36 (No. 1) FORMA, Vol. 36, 2021 (scipress.org)
For the benefit and convenience of readers, this paper is also included in this website.
Research Field [2]
Relationships between the Golden Rectangle, Square-root-of-2 square rectangle, and Golden Square Rectangle
A rectangular parallelepiped has three different faces. In the case of the one called “Square-root-of-2 Rectangular Parallelepiped”, two of these faces are equal to the square-root-of-2 rectangle and the third face is equal to the square-root-of-2 square rectangle. The latter’s two different sides are in the square-root-of-2 square ratio. Here, it is to be noted that the silver square rectangle is composed of one golden rectangle and one golden square rectangle. On the other hand, the one called “Golden Rectangular Parallelepiped”, consists of two golden rectangles and one golden square rectangle. Two different sides of the latter rectangle are in the golden square ratio. Here, it is worth noting that the golden square rectangle consists of one square-root-of-2 square rectangle and one golden rectangle. This means that the golden square rectangle also contains the infinite number of golden rectangles. Golden rectangles line up in sequence alomgside of two different flows, filling in the square-root-of-2 square rectangle. Such relationships are depicted in the following two figures.
Logarithmic Spirals
Logarithmic Spirals already known, a logarithmic spiral is created from the golden rectangle whose side lengths are in the golden ratio. It is also created from the square-root-of-2 rectangle whose side lengths are in the square-root-of-2 ratio. From the square-root-of-2 square rectangle, two new logarithmic spirals are derived.
Research Field [3]
Minimul Surface Area Partition of Space
Four new counter-examples to Kelvin’s conjecture on minimal surfaces have been found. In 1994 Weaire and Phelan discovered a counter-example to Kelvin’s such conjecture whose periodic unit includes two cells of different kind, i.e. the pentagonal dodecahedron and the Goldberg tetrakaidecahedron (hereinafter called WP). It was verified to be more superior to Kelvin’s tetrakaidecahedron in terms of isoperimetric quotient. WP already contained minimum curved surfaces when it was discovered with the help of the Surface Evolver. The four counter-examples presented here didn’t. Therefore, they were initially compared with WP with its faces having been flattened out for planar approximation. Such comparison revealed that the four counter-examples represent partitions with slightly less surface area than the flattened WP structure. In order to enable equivalent comparison, they were then transformed to have minimum curved surfaces included.
This study is described in a mathematical paper “Four New Counter-examples to Kelvin’s Conjucture on Minimul Surface Area Partition of Space” Mathematical paper June 7 2021.
Challenges for the future
The aforementioned special ratios seem to have a close relationship with the cube in the higher-dimensional space. The reasons are as follows:
- If a cube is projected into the three-dimensional space from the four-dimensional space, six-dimensional space, ten-dimensional space, and twelve-dimensional space under certain specific condition, it respectively becomes the rhombic dodecahedron, rhombic triacontahedron, rhombic enneacontahedron, and rhombhecto-triadiohedron.
- The rhombic dodecahedron is composed of 12 square-root-of-2 rhombuses.
- The rhombic triacontahedron is composed of 30 golden rhombuses.
- The rhombic enneacontahedron is composed of 60 silver rhombuses and 30 golden square rhombuses.
The rhombhecto-triadiohedron is of two types and each one consists of three kinds of rhombus. Refer to the sketches below. In view of the above-mentioned facts, these rhombuses are analogized to correspond to either the silver rhombus, golden rhombus, silver square rhombus or the golden square rhombus. However, this has not been confirmed yet. Furthermore, the following points have not been elucidated and they are still veiled in mystery.
- Why a cube in the higher-dimensional space is transformed into a rhombic polyhedron when it is projected into the three-dimensional space under certain specific condition?
- Why such rhombic polyhedron is composed of a rhombus or rhombuses based on the aforementioned special ratio, i.e. the square-root-of-2 rhombus, golden rhombus, square-root-of-2 square rhombus or the golden square rhombus?
To solve some mysteries is my future task.
Archive for the 'Geometry based on Silver Ratio and Golden Ratio' Category

I continue to place my artworks on the exhibition. The one displayed at the exhibition held in Tokyo in early May, 2022 was an illustration of owl. We tend to feel an affinity with owls who are regarded as well-informed being or philosopher in a forest. This illustration was drawn based on the follow-ing geometric figures of various kinds. Face —- Silver rhombus Eye —- Silver spiral, silver rhombus Eyebrow —- Silver rhombus Nose —- Silver rhombus Torso —- Golden ellipse Wave form pattern drawn on the torso —- Either an upper half or lower half of the silver rhombus Wing —- Arc of an ellipse Leg base —- Arc […]
√This art work is a polyhedron with 540 faces. Its origin is the truncated icosahedron that consists of 20 regular hexagons and 12 regular pentagons. If each of regular hexagons and regular pentagons is respectively divided into 6 regular triangles and 5 isosceles triangles, a total of 180 triangles are generated. Furthermore, if each of these triangles is partitioned into 3 triangles, the number of triangles generated becomes 540. Two neighboring triangles basically constitute a tetragon. For the purpose of creating new faces of the solid, all these tetragons are replaced with the golden rhombus. Then, three dimensional rhombic running pattern is created. If each of these rhombuses is partitioned […]

Released on Nov. 11, 2011, the movie titled “Thrive” aims at having all the mankind equally thrive. Anyone, irrespective of age and sex, cannot but feel that argument and issues raised by this movie are significantly related to all aspects of everyday life. It makes a great impact on our perception and awareness. I understand that more than 4 million people have already seen the movie, which is now free to watch online in 17 languages (with more coming soon) at www.thrivemovement.com/the_movie. This movie gives clear and detailed explanations on: (1) fundamental structure of the universe, (2) real existence of technologies to get out free energy that is derived from it, (3) dream […]

Figure 1 Rhombhectotriadio-hedron (T-type) As mentioned in the body text, the rhombhectotriadiohedron (i.e. rhombic polyhedron with 132 faces) is of two types (T and C) and each one is composed of three kinds of rhombus. Please Refer to Figure 1 and Figure 2. My current task is to calculate the angles of these rhombuses by myself. Mr. Yasunari Watanabe who is an excellent researcher on crystallography is well-versed in this geometric field. His paper “Derivation of Some Equilateral Zonohedra and Star Zonohedra” is considered to be highly instrumental in figuring out these angles. It describes the way to build the equilateral-zonogon, star-zonogon, equilateral zonohedra and star zonohedra. First of all, basic plane figures or solids […]

In case of the following galaxies, the angle between the line drawn from the center of the galaxy and the tangent to the sriral is measured to be 72.8 degrees: Great Bear Galaxy M101 — Great Bear [brightness: magnitude 8.2; distance: 19 million light-years] — Pisces [brightness: magnitude 9.8; distance: 37 million light-years] — Canes Venatici [brightness: magnitude 9.0; distance: 21 million light-years], These measurements were made by Mr. Tanimura with his special software “Spiral”. This angle, 72.8 degrees, is about the same as the one of the logarithmic spiral derived from the golden rectangle and the golden rhombas. Please refer to the paper “Logarithmic Spirals based on the Golden Ratio, Golden Square Ratio, Silver Ratio, […]
At the end of June, 2010, the writer newly found out that the combination of the golden rhombus and the silver rhombus enables the plane filling. This fact shows that the Golden Ratio and the Silver Square Ratio are closely related to each other.Earlier in 2009, the writer also discovered the mutually complementary relationship between the Golden Ratio and the Silver Ratio in the 3-dimensional space. Considering this point, this new plane filling seems to indicate that the Golden Ratio and the Silver Square Ratio are mutually complementary to each other in the 2-dimensional plane. As already known, a logarithmic spiral is created from the golden rectangle whose side lengths are […]

The ratio is called the Golden Ratio and the ratio 1 : is called the Silver Ratio. The square of the Silver Ratio is 1:2 and this ratio is called the Silver Square Ratio. On the other hand, a rhombus has a short diagonal and a long diagonal. If the length of these diagonals is in the Golden Ratio, the rhombus is called the Golden Rhombus and, if it is in the Silver Square Ratio, the rhombus is called the Silver Square Rhombus. At the end of June, 2010, the author discovered that the combination of the Golden Rhombus and the Silver Square Rhombus enables the plane filling. This new […]











