• 
• 
• 

日本語 Español 中文 हिन्दी

• 
• 

3D-version of the Japanese Traditional Decorative Pattern

√This art work is a polyhedron with 540 faces. Its origin is the truncated icosahedron that consists of 20 regular hexagons and 12 regular pentagons.  If each of regular hexagons and regular pentagons is respectively divided into 6 regular triangles and 5 isosceles triangles, a total of 180 triangles are generated.  Furthermore, if each of these triangles is partitioned into 3 triangles, the number of triangles generated becomes 540.  Two neighboring triangles basically constitute a tetragon.  For the purpose of creating new faces of the solid, all these tetragons are replaced with the golden rhombus.  Then, three dimensional rhombic running pattern is created. If each of these rhombuses is partitioned into 2 isosceles triangles, a 3D version of Japanese traditional decorative pattern comes into being.

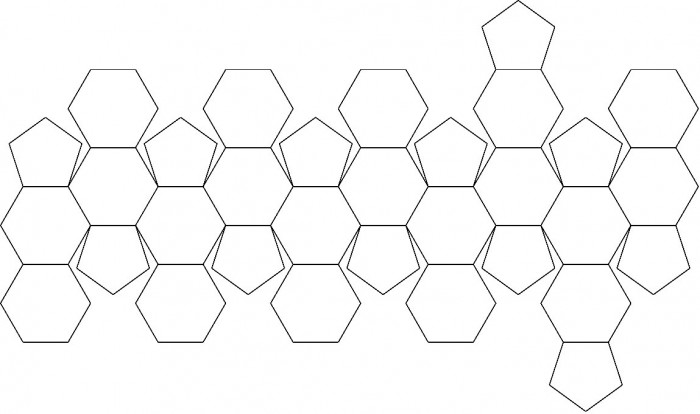
The truncated icosahedron having the same shape as a soccer ball is one of the semiregular polyhedra .  It derives from the regular icosahedron .  It is composed of 20 regular hexagons and 12 regular pentagons.  Shown in Fig. 1 below is a development diagram of the truncated icosahedron.

Fig. 1.  Development diagram of the truncated icosahedron

The regular hexagon can be divided into 6 regular triangles and the regular pentagon can be partitioned into 5 isosceles triangles with the base angle being 54.  If each of the regular hexagons and the regular pentagons of the development diagram is divided into such triangles, a total of 180 triangles are generated as illustratrated in Fig. 2 below.

Fig. 2.  Development diagram with the regular hexagons and pentagons divided into triangles

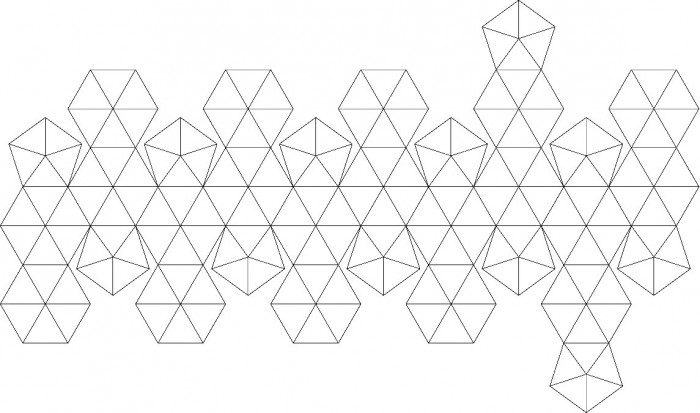
Furthermore, if each of these triangles is partitioned into 3 triangles, the number of triangles generated becomes 540 as depicted in Fig. 3 below .

Fig. 3.  Development diagram with each triangle further divided into 3 smaller triangles

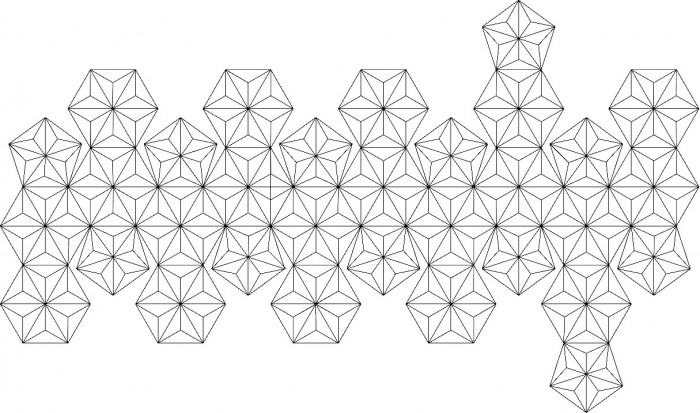
However, new faces cannot be created if partitioning of such polygons is done as they are without any change.  Two neighboring triangles basically constitute a tetragon.  The triangle at the end of the development diagram does not have such neighboring triangle.  However, 2 of these isolated triangles also constitute a tetragon if they are fitted together.  The total number of such tetragons is 270.

For the purpose of creating new faces of the solid, all these tetragons are replaced with the golden rhombus.  The golden rhombus is the one whose length ratio of the shorter diagonal to the longer diagonal is equal to the golden ratio, i.e. 1 : (1+√5)/2.  Its obtuse angle and the acute angle are equal to approximately 116 °33’54.184″ and 63 °26’05.816″, respectively.

Then, three-dimensional rhombic running pattern is created.  If each of these rhombuses is partitioned into 2 isosceles triangles, a 3D-version of the hemp leaf pattern comes into being.  It is one of the representative Japanese traditional decorative patterns.  If this new polyhedron is actually created, its overall form becomes a regular icosahedron as shown in Fig. 4 below.  The reason is that it is originally based on the truncated icosahedron that derives from the regular icosahedron having 12 vertices.  The shape of its twelve vertices are predicated on the regular pentagon and each of its 20 faces contains 27 isosceles triangles.

 

 Fig. 4.  New polyhedron based on a 3D-version of the hemp leaf pattern

Contribution date:2020/09/02　|　Category:Geometry based on Silver Ratio and Golden Ratio